5. 例題: 片持ち梁の計算¶

5.1. 静解析¶

図の様な部材の曲げに対する強度を調べます。この部材は下記の材料で作成されています。

物性値(材料特性) - 鉄 -

項目	値
ヤング率	1.96×10^4 kg/mm^2
ポアソン比	0.3
質量密度	8.01×10^-10 kg・s^2/mm^4

計算の仮定を行います。

部材全体を計算対象とする
上端に1.0kgの荷重をかける
下端を完全に固定する
計算の結果は変位量によって評価する

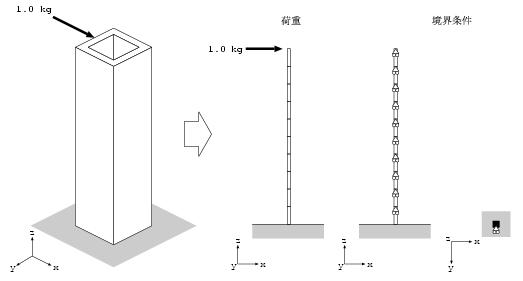
モデル化を行ない、計算条件を決定します。 * 荷重
1.0kgの荷重は集中荷重とします

境界条件
下端の自由度 $X, Y, Z, \theta_x, \theta_y, \theta_z$ を拘束する計算対象の変形に必要のない自由度 $Y, \theta_x, \theta_z$ を拘束するせん断変形と仮定し自由度Zを拘束する
構造
梁要素でモデル化し、形状は断面積、断面2次モーメントで考慮する長さ方向に10分割のメッシュを作成する
構造梁要素でモデル化し、形状は断面積、断面2次モーメントで考慮する長さ方向に10分割のメッシュを作成する

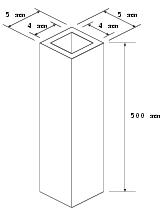
梁要素を使用するために形状特性を定義する必要があります。今回の計算では断面積と断面2次モーメントが必要になりますので下記の計算で求めます。

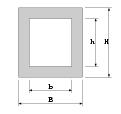
断面積の計算

A = BH - bh
  = 5×5 - 4×4
  = 9.0 mm^2

断面2次モーメントの計算

I = BH^3-bh^3/12
  = 5×5^3-4×4^3/12
  = 30.75 mm^4

形状特性

項目	値
断面積	9.0 mm^2
断面2次モーンメント	30.75 mm^4

以下にデータを示します。この例題は、第2章のデータ作成の例題と同一データです(CCは一部の変更があります)。

ASSIGN OUTPUT2='ex1.op2',UNIT=12
ID   NASTRAN,2005
TIME 10
SOL  101
CEND
TITLE      = STATIC ANALYSIS SOL101
SUBTITLE   = BAR BENDING
SUBCASE 1
LABEL      = CASE 1 (GID:111 FORCE:1.0)
   LOAD    = 1000
   SPC     = 2000
 OUTPUT
   DISPLACEMENT = ALL
   STRESS       = ALL
BEGIN BULK
$
$ PARAMATER
$
PARAM,       POST,     -1
PARAM,    AUTOSPC,    YES
$
$ PROPERTY
$
PBAR,        1000,    1000,   9.0,   30.75,   30.75
MAT1,        1000, 1.96E+4,      ,   0.3, 8.01-10
$
$ LOAD
$
FORCE,       1000,     111,      ,   1.0,     1.0,     0.0,     0.0
$
$ BOUNDARY
$
SPC1,        2000,   123456,      101,
SPC1,        2000,      246,      102,     THRU,     111
SPC1,        2000,        3,      102,     THRU,     111
$
$ MODEL
$
GRID,        101,     ,          0.0,      0.0,       0.0
GRID,        102,     ,          0.0,      0.0,      50.0
GRID,        103,     ,          0.0,      0.0,     100.0
GRID,        104,     ,          0.0,      0.0,     150.0
GRID,        105,     ,          0.0,      0.0,     200.0
GRID,        106,     ,          0.0,      0.0,     250.0
GRID,        107,     ,          0.0,      0.0,     300.0
GRID,        108,     ,          0.0,      0.0,     350.0
GRID,        109,     ,          0.0,      0.0,     400.0
GRID,        110,     ,          0.0,      0.0,     450.0
GRID,        111,     ,          0.0,      0.0,     500.0
$
CBAR,        101,      1000,   101,     102,      0.0,       1.0,       0.0
CBAR,        102,      1000,   102,     103,      0.0,       1.0,       0.0
CBAR,        103,      1000,   103,     104,      0.0,       1.0,       0.0
CBAR,        104,      1000,   104,     105,      0.0,       1.0,       0.0
CBAR,        105,      1000,   105,     106,      0.0,       1.0,       0.0
CBAR,        106,      1000,   106,     107,      0.0,       1.0,       0.0
CBAR,        107,      1000,   107,     108,      0.0,       1.0,       0.0
CBAR,        108,      1000,   108,     109,      0.0,       1.0,       0.0
CBAR,        109,      1000,   109,     110,      0.0,       1.0,       0.0
CBAR,        110,      1000,   110,     111,      0.0,       1.0,       0.0
$
ENDDATA

出力結果
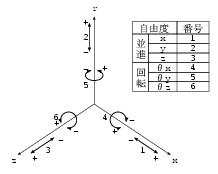
変位は節点データで指定した変位座標で結果出力リスト(f06ファイル)に出力されます。例題の変位座標は基本座標を選択していますので、並進変位 $x, y, z$ が $T_1, T_2, T_3$ 、回転変位 $\theta_x, \theta_y, \theta_z$ が $R_1,R_2,R_3$ に対応します。荷重点の変位を例にすると、節点番号の111番が荷重点なのでPOINT ID.が111、 TYPEがGの行が変位結果となります。並進方向 $x$ に69.13mmの変位で理論値と一致します。

理論値を示します。

変位 = Fl^3/3EI
     = 1.0×500^3/3×1.96×10^4×30.75
     = 69.13334439 mm

F: 荷重 kg
l: 完全固定点からの距離 mm
E: ヤング率 kg/mm^2
I:断面2次モーメント mm^4
結果出力リストを御参照下さい。
結果出力リスト(f06ファイル)

TATIC ANALYSIS SOL101                                                    JUNE  22, 2011  MD NASTRAN   7/ 9/10   PAGE     8
      BAR BENDING
0     CASE 1 (GID:111 FORCE:1.0)                                                                             SUBCASE 1

                                             D I S P L A C E M E N T   V E C T O R

      POINT ID.   TYPE          T1             T2             T3             R1             R2             R3
           101      G      0.0            0.0            0.0            0.0            0.0            0.0
           102      G      1.002434E+00   0.0            0.0            0.0            3.940601E-02   0.0
           103      G      3.871467E+00   0.0            0.0            0.0            7.466401E-02   0.0
           104      G      8.399701E+00   0.0            0.0            0.0            1.057740E-01   0.0
           105      G      1.437974E+01   0.0            0.0            0.0            1.327360E-01   0.0
           106      G      2.160417E+01   0.0            0.0            0.0            1.555500E-01   0.0
           107      G      2.986560E+01   0.0            0.0            0.0            1.742160E-01   0.0
           108      G      3.895664E+01   0.0            0.0            0.0            1.887340E-01   0.0
           109      G      4.866988E+01   0.0            0.0            0.0            1.991040E-01   0.0
           110      G      5.879791E+01   0.0            0.0            0.0            2.053260E-01   0.0
           111      G      6.913335E+01   0.0            0.0            0.0            2.074000E-01   0.0

5.2. 固有値解析¶

静解析で使用した部材について固有振動数を求めたい場合には以下のデータを使用します。静解析と比較して、多少のデータ変更で別の解析機能が利用できることがわかります。強調部分がデータ変更された部分です。固有振動数はランチョス法で3モード迄求める指定になっています。 /apps/t3/sles12sp2/isv/samples/nastran/test7-2.dat に同じファイルが置いてありますので、実行する際はコピーしてご利用ください。

ASSIGN OUTPUT2='ex2.op2',UNIT=12
ID   NASTRAN,2005
TIME 10
SOL  103
     ^^^
CEND
TITLE      = EIGEN VALUE ANALYSIS SOL103
             ^^^^^^^^^^^^^^^^^^^^^^^^^^^
SUBTITLE   = BAR FREQUENCY
             ^^^^^^^^^^^^^
LABEL      = CASE 1
             ^^^^^^
   METHOD  = 1000
   ^^^^^^^^^^^^^^
   SPC     = 2000
 OUTPUT
   VECTOR  = ALL
   ^^^^^^^^^^^^^
BEGIN BULK
$
$ PARAMATER
$
PARAM,       POST,     -1
PARAM,    AUTOSPC,    YES
$
$ PROPERTY
$
PBAR,        1000,    1000,   9.0,   30.75,   30.75
MAT1,        1000, 1.96E+4,      ,   0.3, 8.01-10
$
$ EIGEN VECTOR
$
EIGRL,       1000,    0.0,       ,      3
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
$
$ BOUNDARY
$
SPC1,        2000,   123456,      101,
SPC1,        2000,      246,      102,     THRU,     111
SPC1,        2000,        3,      102,     THRU,     111
$
$ MODEL
$
GRID,        101,     ,          0.0,      0.0,       0.0
GRID,        102,     ,          0.0,      0.0,      50.0
GRID,        103,     ,          0.0,      0.0,     100.0
GRID,        104,     ,          0.0,      0.0,     150.0
GRID,        105,     ,          0.0,      0.0,     200.0
GRID,        106,     ,          0.0,      0.0,     250.0
GRID,        107,     ,          0.0,      0.0,     300.0
GRID,        108,     ,          0.0,      0.0,     350.0
GRID,        109,     ,          0.0,      0.0,     400.0
GRID,        110,     ,          0.0,      0.0,     450.0
GRID,        111,     ,          0.0,      0.0,     500.0
$
CBAR,        101,      1000,   101,     102,      0.0,       1.0,       0.0
CBAR,        102,      1000,   102,     103,      0.0,       1.0,       0.0
CBAR,        103,      1000,   103,     104,      0.0,       1.0,       0.0
CBAR,        104,      1000,   104,     105,      0.0,       1.0,       0.0
CBAR,        105,      1000,   105,     106,      0.0,       1.0,       0.0
CBAR,        106,      1000,   106,     107,      0.0,       1.0,       0.0
CBAR,        107,      1000,   107,     108,      0.0,       1.0,       0.0
CBAR,        108,      1000,   108,     109,      0.0,       1.0,       0.0
CBAR,        109,      1000,   109,     110,      0.0,       1.0,       0.0
CBAR,        110,      1000,   110,     111,      0.0,       1.0,       0.0
$
ENDDATA

結果出力
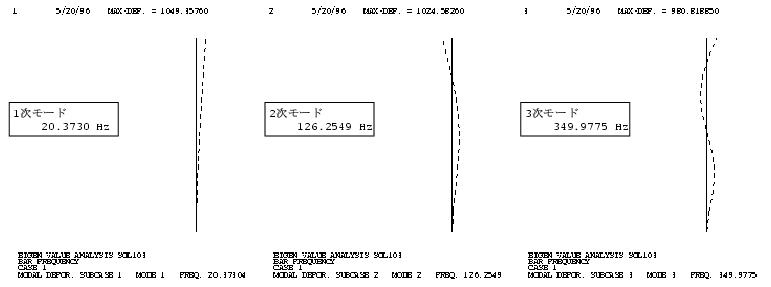
固有振動数は、結果出力リストのCYCLESに出力されています。理論値と計算値の比較を行うと誤差があります。これはデータの要素分割数が粗いためです。精度を良くしたい場合は、要素分割数を増やして下さい。

次数	固有振動数（Hz）理論値	固有振動数（Hz）計算値
1次	20.464246	20.3730
2次	128.2564977	126.2549
3次	359.1580332	349.9775

理論値の計算を示します。
固有振動数 = $\lambda^3 \sqrt{\frac{EIg}{\gamma A}}$
= $\frac{\lambda^3}{(2\pi\times 500^2) } \times \frac{1.96\times 10^4\times 30.75\times g}{8.01 \times 10^-10 \times g} \times 9$

l: 完全固定点からの距離 mm
A: 断面積 mm^2
g: 重力加速度 mm/s^2
E: ヤング率 kg/mm^2
I: 断面2次モーメント mm^4
$\gamma$ : 単位体積の質量 kgf/mm^3
$\lambda$ : 振動係数
1次 $\lambda$ = 1.875
2次 $\lambda$ = 4.694
3次 $\lambda$ = 7.855

モードと出力リストを御参照下さい。

結果出力リスト

1    EIGEN VALUE ANALYSIS SOL103                                               JUNE  22, 2011  MD NASTRAN   7/ 9/10   PAGE     8
      BAR FREQUENCY
0     CASE 1

                                              R E A L   E I G E N V A L U E S
   MODE    EXTRACTION      EIGENVALUE            RADIANS             CYCLES            GENERALIZED         GENERALIZED
    NO.       ORDER                                                                       MASS              STIFFNESS
        1         1        1.638594E+04        1.280076E+02        2.037304E+01        1.000000E+00        1.638594E+04
        2         2        6.292981E+05        7.932831E+02        1.262549E+02        1.000000E+00        6.292981E+05
        3         3        4.835486E+06        2.198974E+03        3.499775E+02        1.000000E+00        4.835486E+06

もっと多くの例題を参照されたい方は、入門例題集、リリースノート、ユーザーガイドを御参照下さい。
ユーザーガイド・リリースノートで使用されている例題の入力ファイルのほとんどが下記ディレクトリに格納されていますので御利用下さい。

/apps/t3/sles12sp2/isv/msc/MSC_Nastran_Documentation/20171/doc/desopt: 設計感度および最適化
/apps/t3/sles12sp2/isv/msc/MSC_Nastran_Documentation/20171/doc/dynamics: 動解析
/apps/t3/sles12sp2/isv/msc/MSC_Nastran_Documentation/20171/doc/linstat: 線形解析
/apps/t3/sles12sp2/isv/msc/MSC_Nastran_Documentation/20171/doc/thermal: 伝熱解析
/apps/t3/sles12sp2/isv/msc/MSC_Nastran_Documentation/20171/doc/relnotes: リリースノート